2020-06-02

数据结构

24 分钟读完 (大约 3598 个字)

红黑树详解

二叉查找树

学习红黑树之前，先理解一下二叉查找树。

二叉查找树（BST）具备什么特性呢？

左子树上所有结点的值均小于或等于它的根结点的值。
右子树上所有结点的值均大于或等于它的根结点的值。
左、右子树也分别为二叉排序树。
查找和插入的过程类似于二分查找的思想，查找所需的最大次数等于二叉树的深度

二叉查找树（BST）缺点有哪些？

主要体现在插入新的节点的时候
假设初始的二叉查找树只有三个结点，根结点值为9，左孩子值为8，右孩子值为12：
接下来我们依次插入如下五个结点：7,6,5,4,3。依照二叉查找树的特性，结果会变成什么样呢？
最终的二叉查找树会非常的不平衡，左子树的深度为6，右边子树的深度为1（一棵好端端的树变成了瘸子，两边的子树不均衡了），这样会导致查找的性能大打折扣，几乎变成了线性查找；

二叉查找树的删除操作

待删除的结点没有子结点：节点没有孩子，因此直接删除即可。
待删除的结点有一个孩子：只有左孩子，于是我们让左孩子结点A取代被删除的结点，结点A以下的结点关系无需变动。（右孩子也是一样的）
待删除的结点有两个孩子：这种情况比较复杂。此时，我们需要选择与待删除结点最接近的结点来取代它。

AVL树与红黑树的差别

AVL是严格平衡的二叉树，要求每个节点的左右子树高度差不超过1；
红黑树更宽松一些，要求任一一条路径的长度都不超过其他路径长度的两倍。
正因为这个差别AVL的查找效率更高，但是平衡调整的成本也更高。在需要频繁查找时，选用AVL树更合适，频繁插入删除时，选用红黑树更合适。

红黑树

目的

红黑树主要是为了解决上面的问题（可以说是一种策略，通过红黑树算法，让二叉查找树变成平衡二叉查找树）

概念

红黑树就是一种平衡的二叉查找树，说他平衡的意思是他不会变成“瘸子”，左腿特别长或者右腿特别长。
红黑树针对AVL树的不足（AVL树删除操作之后的重新平衡可能需要做到多达O(lon n)次旋转，从而频繁地导致全树的整体拓扑结构的大幅变化）进行了改进。
红黑树保证：每次插入或者删除之后的重新平衡过程，全树拓扑结构的更新仅仅涉及常数个节点。尽管最坏情况下也需要对多达O(lon n)个节点重新染色，但是就分摊意义而言，仅仅为O(1)个。
红黑树的适度平衡标准：任一节点左右子树的高度不得超过两倍。（由下面这五条规则来保证）
除了符合二叉查找树的特性之外，还具体下列的特性：

结点是红色或者黑色
根结点是黑色
每个叶子的节点都是黑色的空结点（NULL）//这些是引入的外部节点，使得二叉树扩展为真二叉树
每个红色结点的两个子结点都是黑色的。（从每个叶子到根的所有路径上不能有两个连续的红色结点）
从任意结点到其每个叶子的所有路径都包含相同的黑色结点。

引申:

红节点都是树的内部结点，根节点和外部结点（叶结点）都是黑结点//由第(1)(2)两条规则可知
红节点的孩子不可能是红节点，也就是说红节点的父亲必为黑节点，从每个叶子到根的所有路径上不能有两个连续的红色结点//由第(3)两条规则可知
从根节点到任一节点的途中，黑节点都不少于红节点
从任一节点到其任一后代外部节点的沿途，黑节点的总数亦必相等。//由第(4)两条规则可知

//根节点深度解释为1，更好理解；解释为0，更好计算；我们在这里采用后者
黑深度（black depth）从上向下描述：

从根节点到任一节点的途中，黑节点都不少于红节点，除去根节点本身，沿途所经过的黑节点的总数成为黑深度
所有外部节点的黑深度统一

黑高度（black height）从下向上描述：

从任一节点到其任一后代外部节点的沿途，除去外部节点（黑色），沿途所经过的黑节点的总数称为该节点的黑高度。
所有外部节点的黑高度统一，均为0

插入和删除

当插入和删除节点的时候，红黑树的规则可能会被打破，这时候就需要做出一些调整，从而继续维持我们的规则
什么情况下会破坏红黑树的规则，什么情况下不会破坏规则呢？我们举两个简单的例子：
这个例子去找一下图吧
黑色的NULL节点可忽略
例如上面标准的红黑树，插入值为14的节点。插入之后发现仍然满足红黑树的要求！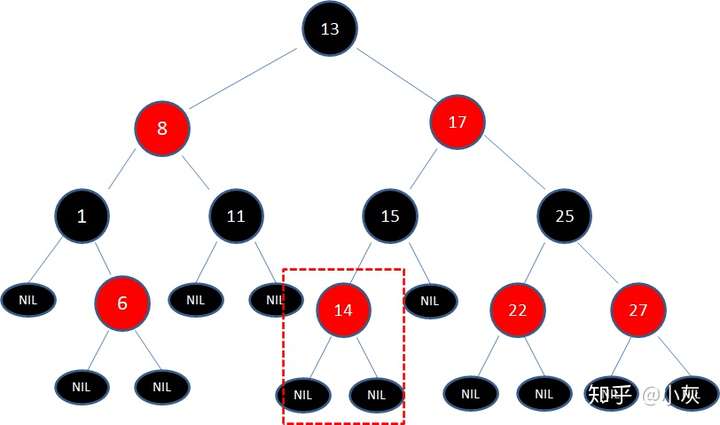

但是如果插入值为21的节点呢？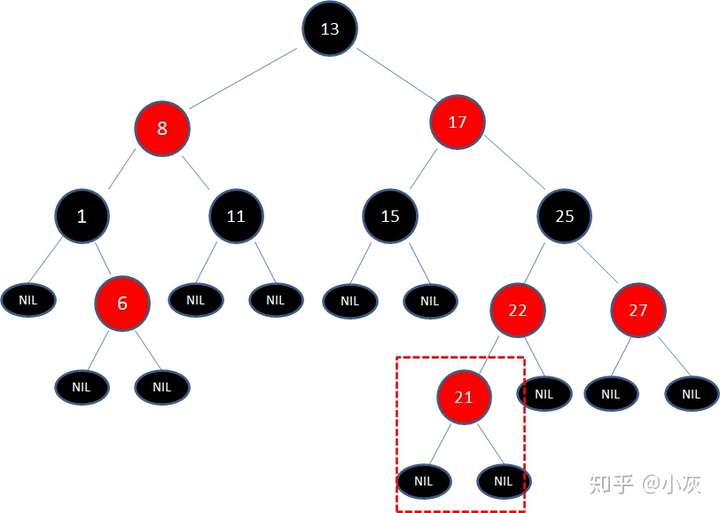

由于父结点22是红色结点（插入的节点默认是红色是因为如果是黑色可能会影响规则5），因此这种情况打破了红黑树的规则4（每个红色结点的两个子结点都是黑色），必须进行调整，使之重新符合红黑树的规则。

调整红黑树的方法

开始玩魔方都是要照着魔方公式一点点玩的，多玩几次就熟悉了。红黑树也和玩魔方一样。
红黑树有两大操作:

recolor (重新标记黑色或红色)
rotation (旋转，这是树达到平衡的关键)
```
- 左旋转 
- 右旋转
```

左旋的示意图

逆时针旋转红黑树的两个结点，使得父结点被自己的右孩子取代，而自己成为自己的左孩子。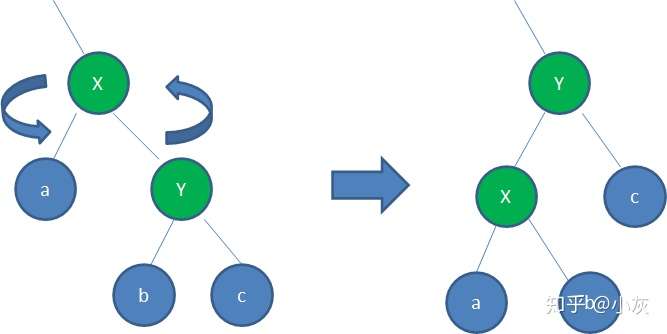
左旋的示意图

右旋的示意图

顺时针旋转红黑树的两个结点，使得父结点被自己的左孩子取代，而自己成为自己的右孩子。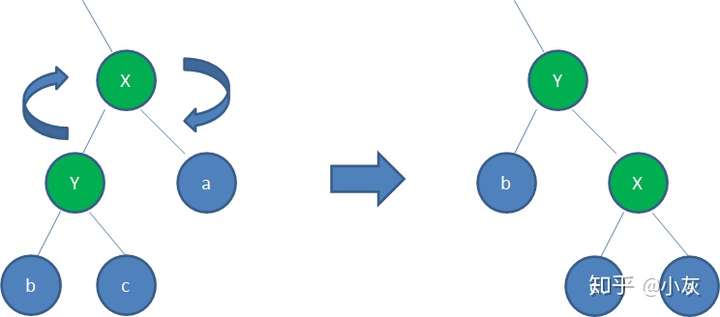
右旋的示意图

示例

为了符合红黑树的规则，会把节点红变黑或者黑变红。
下图展示的是红黑树的部分，需要注意节点25并非根节点。因为21和22链接出现红色，不符合规则4，所以把22红变黑：

但这样还是不符合规则5（但是，仅仅把一个结点变色，会导致相关路径凭空多出一个黑色结点，这样就打破了规则5。），所以需要把25黑变红，看下图：

但是25和27仍然是红色，不满规则4，所以需要将27变为黑色

但这只是局部结束了，全局仍然不能满足条件，15和17仍然是两个连续的红节点，不满足规则4，把17变黑也不行，因为13根节点为黑色，其子节点必为红色。
只能进行旋转了！
按照左旋转，对上边已经变色完成之后图进行左旋转。

旋转之后，由于根节点是红色，需要变黑色

但是仍然不满足规则5，接下来使用右旋转

avatar
最后一个步骤，变色

我晕，这也太复杂了！！！！

红黑树插入节点的5种情况

新结点（A）位于树根，没有父结点。 //这种局面，直接让新结点变色为黑色，
新结点（B）的父结点是黑色。 //这种局面，新插入的红色结点B并没有打破红黑树的规则，所以不需要做任何调整。
新结点（D）的父结点和叔叔(父节点的兄弟)结点都是红色。 //参照下面的总结
新结点（D）的父结点是红色，叔叔结点是黑色或者没有叔叔，且新结点是父结点的右孩子，父结点（B）是祖父结点的左孩子。
4.1 以结点B为轴，做一次左旋转，使得新结点D成为父结点，原来的父结点B成为D的左孩子,变成了局面5.
新结点（D）的父结点是红色，叔叔结点是黑色或者没有叔叔，且新结点是父结点的左孩子，父结点（B）是祖父结点的左孩子。
5.1 我们以结点A为轴，做一次右旋转，使得结点B成为祖父结点，结点A成为结点B的右孩子。接下来，我们让结点B变为黑色，结点A变为红色。

红黑树，超强动静图详解，简单易懂
概括起来就是
假设我们插入的新节点为 X

将新插入的节点标记为红色
如果 X 是根结点(root)，则标记为黑色

如果 X 的 parent 不是黑色，同时 X 也不是 root:
3.1. 如果 X 的 uncle (叔叔) 是红色

3.11.  将 parent 和 uncle 标记为黑色
3.12. 将 grand parent (祖父) 标记为红色
3.13. 让 X 节点的颜色与 X 祖父的颜色相同，然后重复步骤 2、3

3.2. 如果 X 的 uncle (叔叔) 是黑色，我们要分四种情况处理。//刚刚说了 X 的 uncle 是红色的情况，接下来要说是黑色的情况

3.21.  左左 (P 是 G 的左孩子，并且 X 是 P 的左孩子)
3.22.  左右 (P 是 G 的左孩子，并且 X 是 P 的右孩子)
3.23.  右右 (和 3.21镜像过来，恰好相反)
3.24.  右左 (和 3.22镜像过来，恰好相反)

上面的描述过于复杂，还是看图解吧！漫画：什么是红黑树？（完整版）

红黑树删除节点的5种情况

第一步：如果待删除结点有两个非空的孩子结点，转化成待删除结点只有一个孩子（或没有孩子）的情况。

第二步：根据待删除结点和其唯一子结点的颜色，分情况处理。

自身是红色，子结点是黑色：
自身是黑色，子结点是红色：
自身是黑色，子结点也是黑色，或者子结点是空叶子结点：

第三步：遇到双黑结点，在子结点顶替父结点之后，分成6种子情况处理。

结点2是红黑树的根结点：
结点2的父亲、兄弟、侄子结点都是黑色：
结点2的兄弟结点是红色：
结点2的父结点是红色，兄弟和侄子结点是黑色：
结点2的父结点随意，兄弟结点B是黑色右孩子，左侄子结点是红色，右侄子结点是黑色：
结点2的父结点随意，兄弟结点B是黑色右孩子，右侄子结点是红色：