B树与B+树详解

基本概念

多路搜索树（multi-way search tree）：

• 将传统的二叉搜索树，改造为多路搜索树——在中序的遍历下，这也是一种等价变换
• 以k层为间隔如此重组，可以将二叉搜索树转化为等价的2^k路搜索树，统称为多路搜索树。
• 多路搜索树同样支持查找等操作，而且效果与原来的二叉树完全等同；但是重要的是，其对外存的访问方式已经发生本质变化，是以大节点为单位从外存读取一组（而不是单个）关键码。

B树就是B-树：

• B-树就是B树，中间的横线不是减号，直接读成B树即可。
• 有的文章里出现的B-树，即为B树。因为B树的原英文名称为B-tree，而国内很多人喜欢把B-tree译作B-树，而事实上是，B-tree就是指的B树。
• B树是一种多路平衡搜索树，它的每一个节点最多包含K个孩子，k被称为B树的阶。
• k的大小取决于磁盘页的大小
• B树比较矮胖，扁平化，B-树的宽度往往大于其高度

B+树：

• 是应文件系统所需而产生的一种B-tree的变形树。

应用

数据库索引主要基于什么数据结构？
hash表和B+树

数据库索引为什么要用B+树结构来存储呢？
树的查询效率高。而且可以保持有序。但是为什么不用二叉查找树呢？主要是因为磁盘I/O的影响，数据库索引是存储在磁盘上的，当数据量比较大的时候，索引的大小可能有几个G甚至更多。当我们利用索引查询时候，能把整个索引全部加载到内存吗？很显然不可能的，我们能做的是逐一加载每一个磁盘页，这里的磁盘页面对应着索引树的节点。这样的话，每遍历到一个节点就需要进行一次I/O操作。
磁盘这种外部存储器适合批量式的访问，为了减少I/O，我们需要把原本瘦高的树结构变得矮胖，这就是B-树的特征之一。

大规模数据存储中，实现索引查询这样一个实际背景下，树节点存储的元素数量是有限的，如何减少树的深度？
一个基本的想法就是：采用多叉树结构（由于树节点元素数量是有限的，自然该节点的子树数量也就是有限的）

B-树主要应用于文件系统以及部分数据库索引，比如著名的非关系型数据库MongoDB。

B-树（Balance Tree）

所谓m阶B-树，即为m路平衡搜索树（m大于等于2）,除了根节点，各个节点的分支数目介于[M/2向上取整, M]。
M为设定的非叶子结点最多子树个数，N为关键字总数。
由于限制了除根结点以外的非叶子结点，至少含有M/2个儿子，确保了结点的利用率，其最底搜索性能为：O(log n)

1. 根结点至少有两个子女。
2. 子节点数：每个中间节点都包含k-1个元素和k个孩子，其中 m/2 <= k <= m
3. 关键字数：每一个叶子节点都包含k-1个元素，其中 m/2 <= k <= m
4. 所有的叶子结点都位于同一层。叶子节点除了包含了关键字和关键字记录的指针外也有指向其子节点的指针只不过其指针地址都为null（可以把这些null看成外部节点）
5. 排序方式：每个节点中的元素从小到大排列，节点当中k-1个元素正好是k个孩子包含的元素的值域分划。

B-树的特性

1. 关键字集合分布在整颗树中；
2. 任何一个关键字出现且只出现在一个结点中；
3. 搜索有可能在非叶子结点结束；
4. 其搜索性能等价于在关键字全集内做一次二分查找；
5. 自动层次控制；

举一个B-树的例子，一个3阶的B-树，也就是(2,3)-树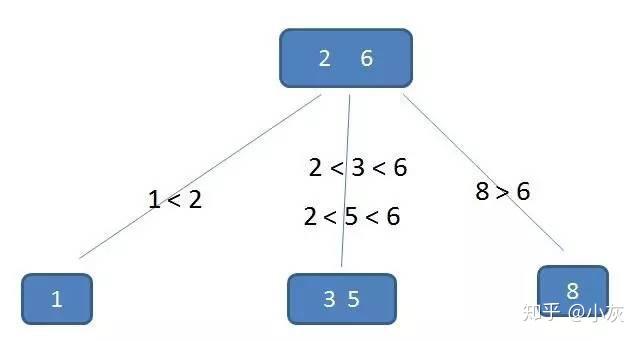

对于这颗树查询的过程比较次数不比二叉查找树少，尤其当单一节点中的元素数量很多的时候，可是相对于磁盘I/O，内存中的比较耗时几乎可以忽略，所以可以提升查找的性能。

B-树插入

优势，自平衡
遵循规则：

1. 节点拆分规则：当前是要组成一个3路查找树，那么此时m=3,关键字数必须<=3-1（这里关键字数>2就要进行节点拆分，拆分的规则是把中间的元素提取出，放到父节点上，左边的单独构成一个节点，右边的单独构成一个节点）；
2. 排序规则：满足节点本身比左边节点大，比右边节点小的排序规则;

自顶向下查找4的节点位置，发现4应当插入到节点元素3，5之间。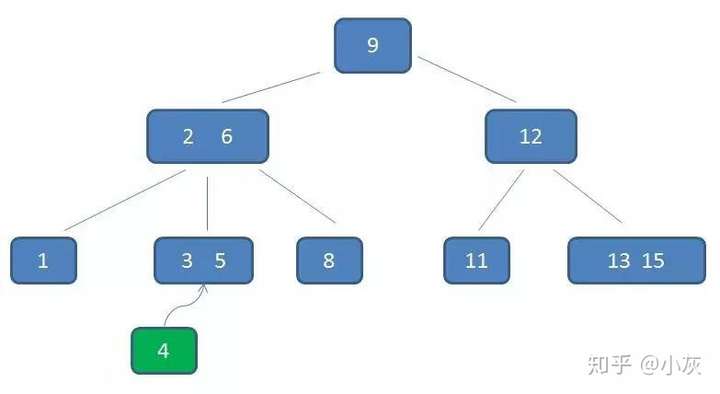

节点3，5已经是两元素节点，无法再增加。父亲节点 2， 6 也是两元素节点，也无法再增加。根节点9是单元素节点，可以升级为两元素节点。于是拆分节点3，5与节点2，6，让根节点9升级为两元素节点4，9。节点6独立为根节点的第二个孩子。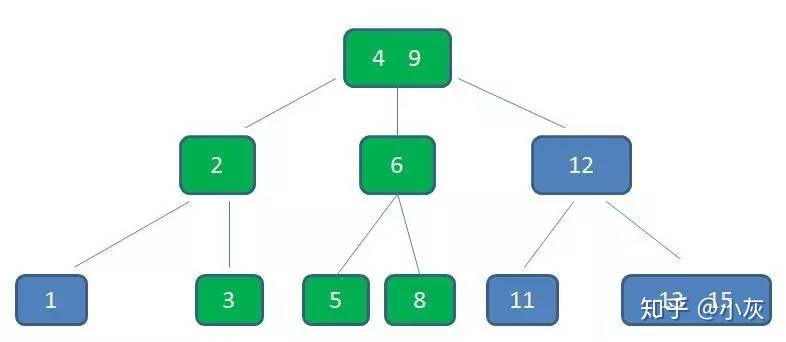

B-树删除

遵循规则：

1. 节点合并规则：当前是要组成一个3路查找树，那么此时m=3,关键字数必须大于等于ceil（3/2）（这里关键字数<1就要进行节点合并）；
2. 满足节点本身比左边节点大，比右边节点小的排序规则;
3. 关键字数小于1时先从子节点取，子节点没有符合条件时就向向父节点取，取中间值往父节点放；

自顶向下查找元素11的节点位置。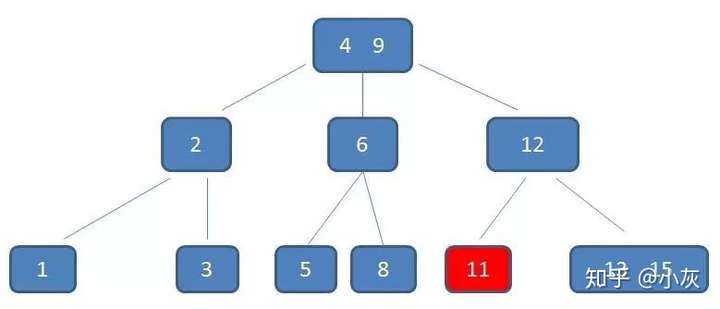

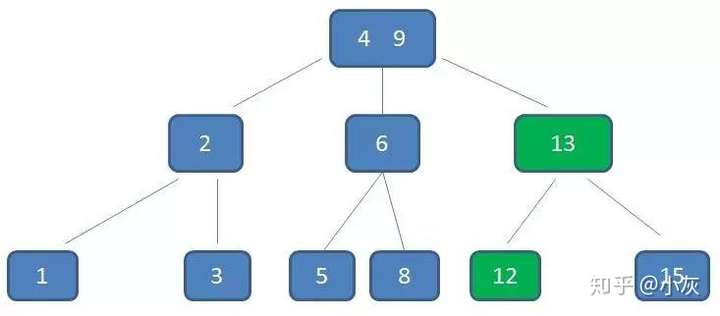
删除11后，节点12只有一个孩子，不符合B树规范。因此找出12,13,15三个节点的中位数13，取代节点12，而节点12自身下移成为第一个孩子。（这个过程称为左旋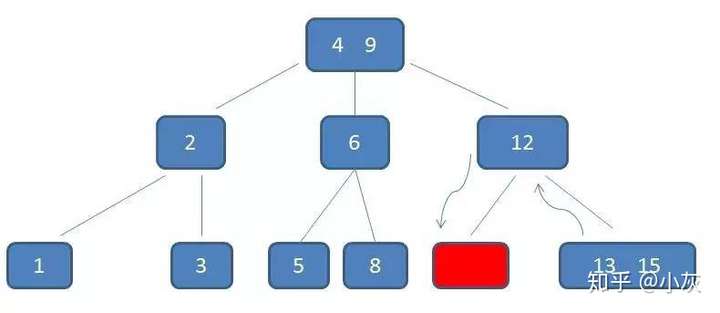

B-树中的卫星数据

卫星数据（Satellite Information）:指的是索引元素所指向的数据记录，比如数据的某一行。在B-树中，无论中间节点还是叶子节点都带有卫星数据。
B-树中的卫星数据（Satellite Information）:无论是叶子节点还是中间节点都带有卫星数据。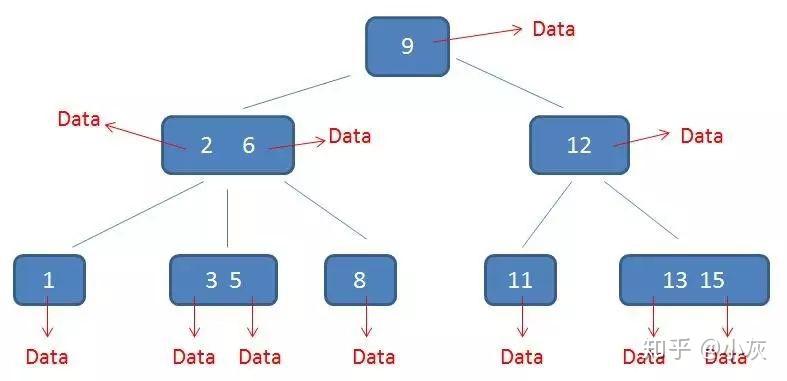

B-树的范围查找过程

比方对于上面的B-树，我们想查找3到11的元素，只能依靠繁琐的中序遍历。

B+树（ Tree）

B+树是B树的一个升级版，相对于B树来说B+树更充分的利用了节点的空间，让查询速度更加稳定，其速度完全接近于二分法查找。
B+树是对B树的一种变形树，它与B树的差异在于：

• 有k个子结点的结点必然有k个关键码；
• 非叶结点仅具有索引作用，跟记录有关的信息均存放在叶结点中。
• 树的所有叶结点构成一个有序链表，可以按照关键码排序的次序遍历全部记录。

一个m阶的B+树具有如下几个特征：

1. 有k个子树的中间节点包含有k个元素（B树中是k-1个元素），每个元素不保存数据，只用来索引，所有数据都保存在叶子节点。
2. 所有的叶子结点中包含了全部元素的信息，及指向含这些元素记录的指针，且叶子结点本身依关键字的大小自小而大顺序链接。
3. 所有的中间节点元素都同时存在于子节点，在子节点元素中是最大（或最小）元素。

示例

B+的特性

1. 所有关键字都出现在叶子结点的链表中（稠密索引），且链表中的关键字恰好是有序的；
2. 不可能在非叶子结点命中；
3. 非叶子结点相当于是叶子结点的索引（稀疏索引），叶子结点相当于是存储（关键字）数据的数据层；
4. 更适合文件索引系统；

B+树插入

B+树中的卫星数据

卫星数据（Satellite Information）:指的是索引元素所指向的数据记录，比如数据的某一行。在B-树中，无论中间节点还是叶子节点都带有卫星数据。
B+树中的卫星数据（Satellite Information）:只有叶子节点带有卫星数据。中间节点仅仅是索引，没有任何关联数据。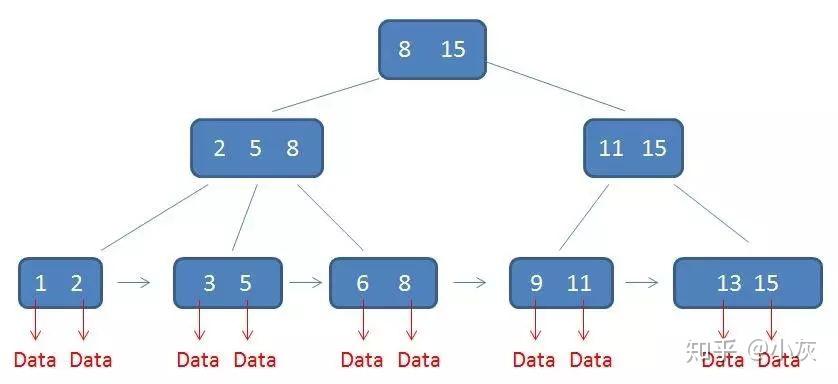

需要补充的是，在数据库的聚集索引（Clustered Index）中，叶子节点直接包含卫星数据。在非聚集索引（NonClustered Index）中，叶子节点带有指向卫星数据的指针。

B+树的范围查找过程

相对于B-树要简单的多，只需要在链表上做遍历即可！

B树与B+树的优点

B+树的优点：
由于B+树在内部节点上不好含数据信息，因此在内存页中能够存放更多的key。 数据存放的更加紧密，具有更好的空间局部性。因此访问叶子几点上关联的数据也具有更好的缓存命中率。
B+树的叶子结点都是相链的，因此对整棵树的便利只需要一次线性遍历叶子结点即可。而且由于数据顺序排列并且相连，所以便于区间查找和搜索。而B树则需要进行每一层的递归遍历。相邻的元素可能在内存中不相邻，所以缓存命中性没有B+树好。

1. B+树的层级更少：单一节点存储更多的元素，使得查询的IO次数更少，相较于B树B+每个非叶子节点存储的关键字数更多，树的层级更少所以查询数据更快；。
2. B+树查询速度更稳定：所有查询都要查找到叶子节点，查询性能稳定。
3. B+树天然具备排序功能：所有叶子节点形成有序链表，便于范围查询。
4. B+树全节点遍历更快：B+树遍历整棵树只需要遍历所有的叶子节点即可，，而不需要像B树一样需要对每一层进行遍历，这有利于数据库做全表扫描。

B树的优点:

1. 由于B树的每一个节点都包含key和value，因此经常访问的元素可能离根节点更近，因此访问也更迅速。

B树和B+树的区别

• B+树的非叶子结点只包含导航信息，不包含实际的值，所有的叶子结点和相连的节点使用链表相连，便于区间查找和遍历。
• B+树只有达到叶子结点才命中（B-树可以在非叶子结点命中），其性能也等价于在关键字全集做一次二分查找；

1. B+树的中间节点没有卫星数据，所以同样大小的磁盘页可以容纳更多的节点元素。这就意味着，数据量相同的情况下，B+树的结构比B树更加矮胖，因此查询时候的I/O次数也越少。
2. B+树的查询必须查到叶子节点，而B-树只要找到匹配元素即可。因此B-树的查找性能并不稳定，最坏情况是查找到叶子节点。而B+树的每一次查找都是稳定的。

为什么说B+树比B树更适合数据库索引？

B+树的磁盘读写代价更低：B+树的内部节点并没有指向关键字具体信息的指针，因此其内部节点相对B树更小，如果把所有同一内部节点的关键字存放在同一盘块中，那么盘块所能容纳的关键字数量也越多，一次性读入内存的需要查找的关键字也就越多，相对IO读写次数就降低了。
B+树的查询效率更加稳定：由于非终结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。
B+树的范围查询更加方便：由于B+树的数据都存储在叶子结点中，分支结点均为索引，方便扫库，只需要扫一遍叶子结点即可，但是B树因为其分支结点同样存储着数据，我们要找到具体的数据，需要进行一次中序遍历按序来扫，所以B+树更加适合在区间查询的情况，所以通常B+树用于数据库索引。
B树在提高了IO性能的同时并没有解决元素遍历的我效率低下的问题，正是为了解决这个问题，B+树应用而生。B+树只需要去遍历叶子节点就可以实现整棵树的遍历。而且在数据库中基于范围的查询是非常频繁的，而B树不支持这样的操作或者说效率太低。

总结

B-树和B+树都是很基础的概念，需要掌握好啊！

二叉搜索树：

• 二叉树，每个结点只存储一个关键字，等于则命中，小于走左结点，大于走右结点；

B（B-）树：

• 多路搜索树，每个结点存储M/2到M个关键字，非叶子结点存储指向关键字范围的子结点；
• 所有关键字在整颗树中出现，且只出现一次，非叶子结点可以命中；

B+树：

• 在B-树基础上，为叶子结点增加链表指针，所有关键字都在叶子结点中出现，非叶子结点作为叶子结点的索引；B+树总是到叶子结点才命中；

B*树：

• 在B+树基础上，为非叶子结点也增加链表指针，将结点的最低利用率从1/2提高到2/3

参考资料

漫画：什么是B+树？
从B树、B+树、B*树谈到R 树
平衡二叉树、B树、B+树、B*树 理解其中一种你就都明白了
漫画：什么是B-树？
从二叉查找树到B+树中间的各种树 //写的相当不错
B-树 百度百科
阿里面试，问了B+树，这个回答让我通过了
数据结构 邓俊辉